Naive Bayes from scratch

The title summarizes well the subject of this project. Implementation from scratch is the best way to truly understand a model (although intimidating initially). The project helped me learn how to apply data pre-processing and improve my Python programming skills.

This study shows the analysis of Gaussian naive Bayes to predict the abalone age [Y. Han, 2019]. The nature of labeling an abalone being older than 9 years old or not given a set of physical measurements is a valuable task for both farmers and customers. To determine the price of the shellfish, farmers estimate the abalone’s age by cutting the shells and counting the rings through the microscope, a very complex and costly method due to the variation in their size and growth characteristics.

Naive Bayes Classifier

We will first start with naive Bayes classifier (NBC). Recall, if the features are mutually-independent. Then NBC estimates the prior probabilities of each hypothesis and the probability of each instance.

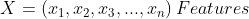
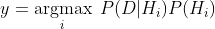
Notice, the product can lead to numbers approaching 0 which will cause underflow. The latter term refers to the event when a floating-point data runs out of precision due to extremely tiny numbers. The common work around is to use log-probabilities.

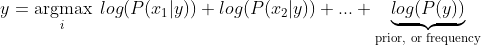
We now observe the simple task left ahead. Build the necessary framwork to evaluate the max posterior and the classifier will have accomplished its role.

        # Prob of binary categorical number of occurences/total
        for col in cat.columns:
            unique = cat[col].value_counts()
            unique = unique.apply(lambda x: x/class_count)
            self.likelihoods[s][col] = unique

        # Prob of binary
        for col in bin.columns:
            unique = bin[col].value_counts()
            unique = unique.apply(lambda x: x / class_count)
            self.likelihoods[s][col] = unique

        self.priors[s] = class_count / float(num_samples)

    def max_posterior(self, [...]):
        posteriors = []
        # probability for each class
        for i in self._classes:
            prior = np.log(self.priors[i])
            # sum of all the n feature probabilities
            cont_likelihood = np.log(self.normal(i, cont))
            cont_likelihood = np.sum(cont_likelihood[~np.isnan(cont_likelihood)])
            cat_likelihood = np.sum(np.log(self.categorical_likelihood(i, cat)))
            bin_likelihood = np.sum(np.log(self.categorical_likelihood(i, bin)))
            likelihood = cont_likelihood + cat_likelihood + bin_likelihood
            posterior = prior + likelihood
            # posteriors contain the probabilities of the two labels for each instance
            posteriors.append(posterior)

        return self._classes[np.argmax(posteriors)]

Data Preprocessing

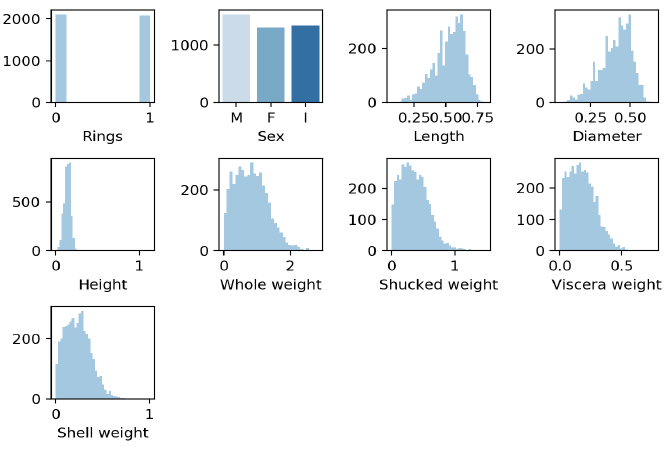
Data transformation by standardization is applied since it has been shown to speed up convergence via gradient descent [ S. Ioffe and C. Szegedy, 2015] and implicitly balances the contribution of all features. The shellfish abalone rings label with values ranging from 4 to 22 years old was binarized into 1 for all values 9 years old and younger and 0 for all values older than 9 years old. Standardization is also required for proper L2 regularization model. Thus, the data set is the outcome of data cleaning, relevance analysis, data transformation and data reduction.

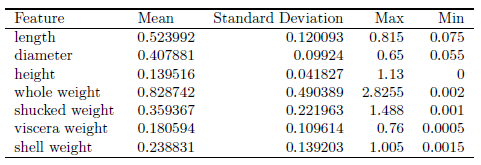
Results

After hyperparameter tuning, Naive Bayes is trained on the entire train split and tested on the unseen test split for all data sets. The model was first validated using 5 fold cross validation; then trained on the train split and evaluated on the test split.

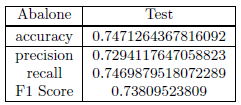
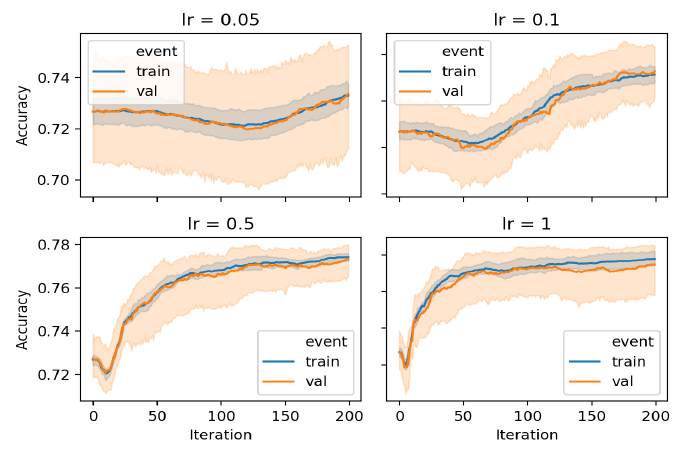
To view the result on the other dataset I welcome you to visit my Github repo.

Sources